Clover: A Trifecta of Vendor-Agnostic, GPU-Accelerated Numerical Libraries

By Rob Farber, contributing writer

Numerical libraries have an enormous impact on scientific computing because they act as the gateway middleware that enables many applications to run on state-of-the-art hardware. Algorithmic and implementation advances in these libraries can increase the speed and accuracy of many modeling and simulation packages and can provide access to new computational systems.

Part of the magic of mathematics is that the same mathematical methods can be applied to wildly disparate physical phenomena. Examples include linear algebra and the fast Fourier transform (FFT). This generality is the foundation upon which numerical libraries are built. A well-designed numerical library also provides an abstraction layer via an API in such a way that users need only focus on their research and not on the computational platform. Such is the case with the Computational Libraries Optimized via Exascale Research (CLOVER) project.

Figure 1. Hartwig Anzt.

Encompassing three foundational libraries, the Exascale Computing Project’s (ECP’s) CLOVER team has brought GPU acceleration to the Software for Linear Algebra Targeting Exascale (SLATE) library for dense linear algebra, to Ginkgo for sparse linear algebra, and to the highly efficient FFTs for exascale (heFFTe) library for CPU- and GPU-accelerated, multinode, multidimensional FFTs. These libraries provide scientists around the world with access to the latest in GPU-accelerated computing—whether the application is running on an exascale system, on a computational cluster, or locally on a GPU-accelerated laptop or workstation.

Preliminary results demonstrate that CLOVER users can run efficiently on AMD, NVIDIA, and Intel GPU-accelerated systems. These benchmarks also demonstrate performance parity with AMD, NVIDIA, and Intel vendor library implementations on some computational kernels. In the race for performance portability, Hartwig Anzt (Figure 1)—director of the Innovative Computing Laboratory, professor in the Min H. Kao Department of Electrical Engineering and Computer Science (EECS) at the University of Tennessee, and research group leader at the Karlsruhe Institute of Technology—observed, “Software lives longer than hardware. Our team is working to avoid library death through good design.”

Software lives longer than hardware. Our team is working to avoid library death through good design. — Hartwig Anzt

Scalability and performance are essential to achieving exascale performance. To this end, benchmark results demonstrate that the heFFTe library can scale to support production runs on the Frontier exascale system after it passes its ready-for-production acceptance tests. The heFFTe team conducted these benchmarks on Crusher, which is an early access test-bed system built with hardware identical to that of the Frontier supercomputer and designed with similar software.[1],[2]

Technology Introduction

Linear algebra provides scientists with a language to describe space and the manipulation of space by using numbers that can be calculated on a computer. Specifically, linear algebra is about performing linear combinations of operations, or linear transforms, by using arithmetic operations on columns of numbers (i.e., vectors) and arrays of numbers (i.e., matrices) to create new, more meaningful vectors and matrices. Based on such linear algebra calculations, scientists can glean useful information about speed, distance, or time in a physical space. Alternatively, scientists can use these calculations in an abstract space to perform a linear regression, which is a valuable tool used to predict data related to decision-making, medical diagnosis, and statistical inference. The Google PageRank algorithm used by search engines provides a common example of the power of linear algebra and eigenvalues. The 3Blue1Brown video “Essence of Linear Algebra Preview” briefly introduces linear algebra for a general technical audience.

Normally, the choice of technique and library depends on the type of matrix being targeted. For example, the SLATE library is designed to operate on dense matrices, in which most or all the elements in the matrix are nonzero. Arithmetic operations on these types of matrices tend to be computationally intensive, so users can expect higher performance on a GPU. The Ginkgo library, by contrast, is designed to operate on sparse matrices, in which few elements in the matrix are nonzero. Operations on sparse matrices tend to be bound by memory bandwidth when accessing nonzero matrix elements and limited by memory capacity when an operation creates many nonzero matrix entries. Through smart design techniques, the Ginkgo team maximized the use of the GPU memory subsystem to achieve performance competitive with vendor-optimized, sparse matrix kernels. Ginkgo has a huge advantage over vendor libraries because it is GPU agnostic, so scientists are not locked into a specific vendor implementation or hardware.

The FFT has been described as “the most important numerical algorithm of our lifetime,”[3] and the Institute of Electrical and Electronics Engineers (IEEE) magazine, Computing in Science & Engineering, included it in the top 10 algorithms of the twentieth century.[4] It is used in many domain applications, including molecular dynamics, spectrum estimation, fast convolution and correlation, signal modulation, and wireless multimedia. The heFFTe website that more than a dozen Exascale Computing Project (ECP) applications use FFT in their codes.[5] The 3Blue1Brown video, “But What Is the Fourier Transform? A Visual Introduction,” provides an overview of this important algorithm for a general audience.

The heFFTe library revisited the design of existing FFT libraries to develop a distributed, 3D FFT library and robust 2D implementations that can support applications that run on large-scale, heterogeneous systems with multicore processors and hardware accelerators. For example, the heFFTe team has focused on implementing a scalable, GPU-enabled, and performance-portable 3D FFT. Distributed 3D FFTs are one of the most important kernels in molecular-dynamics computations, and the performance of these FFTs can drastically affect an application’s ability to run on larger machines. Additionally, the redesign effort was a codesign activity that involved other ECP application developers.[6] For more information, see “heFFTe—A Widely Applicable, CPU/GPU, Scalable Multidimensional FFT That Can Even Support Exascale Supercomputers.”

Anzt recognized the importance of lessons learned from the community-based Extreme-scale Scientific Software Development Kit (xSDK) and Extreme-scale Scientific Software Stack (E4S) projects. He emphasized that API design and user feedback go hand in hand. Furthermore, continuous integration (CI) is essential to ensure library performance and correctness on all supported systems. CI also frees development from the constraints of legacy algorithms and code decisions, as highlighted in the ECP article, “High-Accuracy, Exascale-Capable, Ab Initio Electronic Structure Calculations with QMCPACK: A Use Case of Good Software Practices.”

Technical Discussion

Each of the three libraries in the CLOVER project provides essential functionality for a large scientific user base. GPU acceleration is critical to achieving high performance on exascale supercomputers. Performance benchmarks demonstrate that the CLOVER libraries are ready for production runs on the Frontier exascale system. Early results on Intel and AMD GPUs demonstrate that all three libraries will deliver high performance regardless of the GPU vendor.

SLATE

The SLATE library implements a GPU-accelerated, distributed, dense linear algebra library that will replace the Scalable Linear Algebra PACKage (ScaLAPACK).[7] The Linear Algebra PACKage (LAPACK) and ScaLAPACK have been the standard linear algebra libraries for decades, and this success can largely be attributed to the layered software stack (Figure 2) that can call vendor-optimized Basic Linear Algebra Subprograms (BLAS).[8]

Figure 2. The SLATE software stack is designed in layers, thus enabling applications to call device-optimized linear algebra libraries.

SLATE follows this proven paradigm to implement similar ScaLAPACK functionality (e.g., parallel BLAS, norms, solving linear-systems, least squares, eigenvalue problems, singular value decomposition) and to expand coverage to new algorithms.

The goal is to support current hardware (i.e., CPUs and GPUs) and to provide sufficient flexibility to support future hardware designs. The software layers are designed to prevent language lock-in, as successfully demonstrated by current support for Open Multi-Processing (OpenMP), CUDA, ROCm (Radeon Open Compute Platform), and oneAPI. This performance portability is based on the C++ standard library and C++ templates to avoid code duplication.

The Parallelism Model

As stated succinctly in the paper, SLATE: Design of a Modern Distributed and Accelerated Linear Algebra Library, SLATE utilizes three or four levels of parallelism: distributed parallelism between nodes using MPI, explicit thread parallelism using OpenMP, implicit thread parallelism within the vendor’s node-level BLAS, and, at the lowest level, vector parallelism for the processor’s SIMD vector instructions. For multicore, SLATE typically uses all the threads explicitly, and uses the vendor’s BLAS in sequential mode. For GPU accelerators, SLATE uses a batch BLAS call, utilizing the thread-block parallelism built into the accelerator’s BLAS. The cornerstones of SLATE are 1) the SPMD programming model for productivity and maintainability, 2) dynamic task scheduling using OpenMP for maximum node-level parallelism and portability, 3) the lookahead technique for prioritizing the critical path, 4) primarily reliance on the 2D block cyclic distribution for scalability, 5) reliance on the gemm operation, specifically its batch rendition, for maximum hardware utilization. A task graph of the Cholesky factorization demonstrates the basic framework, as shown in Figure 3.

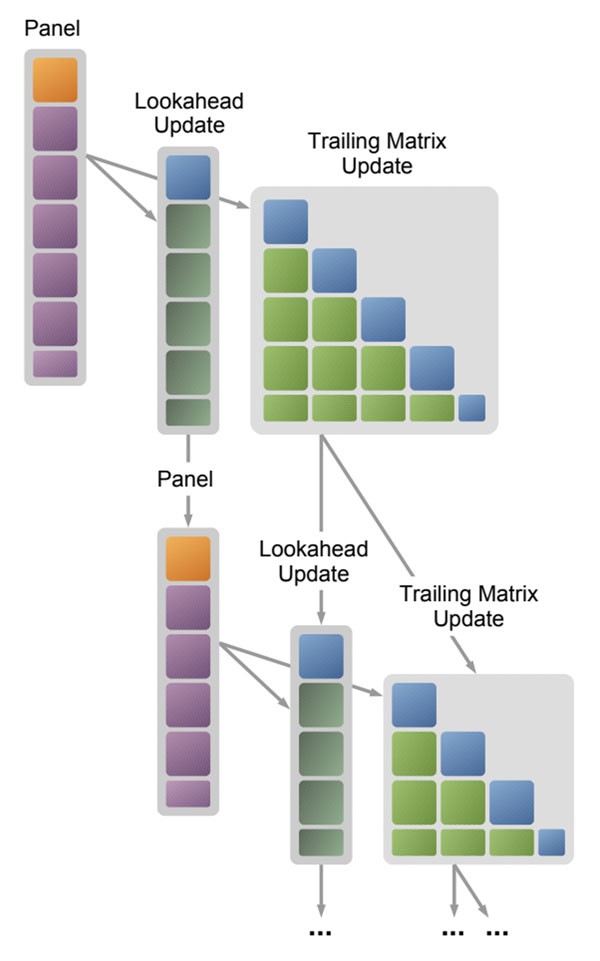
Figure 3. Tasks in Cholesky factorization. Arrows depict dependencies. Source

Expanded Coverage to New Algorithms

Anzt noted that the testing on GPUs yielded a big performance boost that increased with problem size. This is a remarkable achievement. Furthermore, it constitutes a use case of how other high-performance computing (HPC) projects can leverage GPUs to gain better scalability and on-node performance.

Computer scientists use big-O notation to describe the execution time required, or the space used, by an algorithm in terms of how quickly the execution time or space usage grows with the input size. Using N to indicate the input size, Anzt observed that the run time on GPUs transitioned from linear, denoted as O(N), to sublinear, in which the execution grew more slowly than the size of the problem (Figures 4 and 5). This sublinear run-time behavior is largely attributable to the massive parallelism of the GPU coupled with the team’s innovative software design.

SLATE creates a directed acyclic graph (DAG) and uses it to make run-time decisions to exploit overlapped computation and parallelism and, when available, mixed precision. The DAG also aids the decision of which section of code should run on the GPU, rather than the CPU, to achieve the best performance. The Parallel Runtime Scheduling and Execution Controller (PaRSEC) project also uses DAGs to optimize performance. At SC22, PaRSEC was used in a Gordon Bell Prize finalist paper, “Reshaping Geostatistical Modeling and Prediction for Extreme-Scale Environmental Applications.”

DAGs Provide an Excellent Use Case for Other HPC Projects

Figures 4 and 5 highlight the impact of SLATE and the use of DAGs on the run time of two common operations of dense linear algebra. These graphs report the run time of ScaLAPACK and SLATE for a matrix-matrix multiply (dgemm) and a Cholesky factorization (dpotrf) when using a CPU and when using an NVIDIA P100 GPU.[9] Note the extraordinary increase in performance as the problem size increased. This graph illustrates Anzt’s point that scaling on GPUs demonstrates better-than-linear scaling run-time behavior.

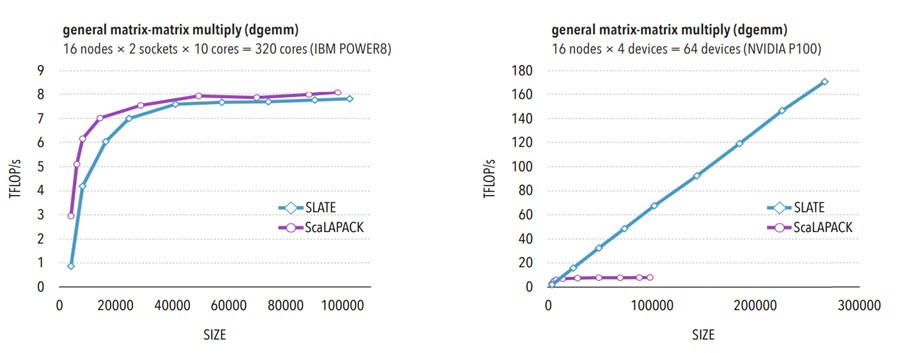
Figure 4. Performance of matrix-matrix multiply (dgemm) without acceleration (left) and with acceleration (right).

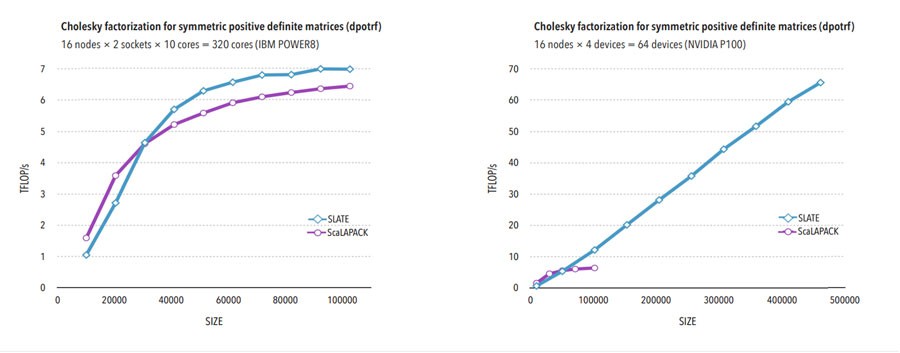
Figure 5. Performance of Cholesky factorization (dpotrf) without acceleration (left) and with acceleration (right).

GPU-Aware MPI Portability Issues

In addition to providing GPU acceleration, SLATE is designed to run efficiently in a distributed computing environment, so the MPI library and communications fabric can heavily influence the library’s performance. As the Crusher test bed demonstrated, using SLATE with an optimized GPU-aware MPI implementation boosts performance (Figures 6 and 7). These results show superior weak-scaling performance for gemm and potrf operations. Unfortunately, the SLATE team noted that there is no portable way to enable GPU-aware MPI in SLATE. Instead, users must specify this choice in their job-scheduling script.

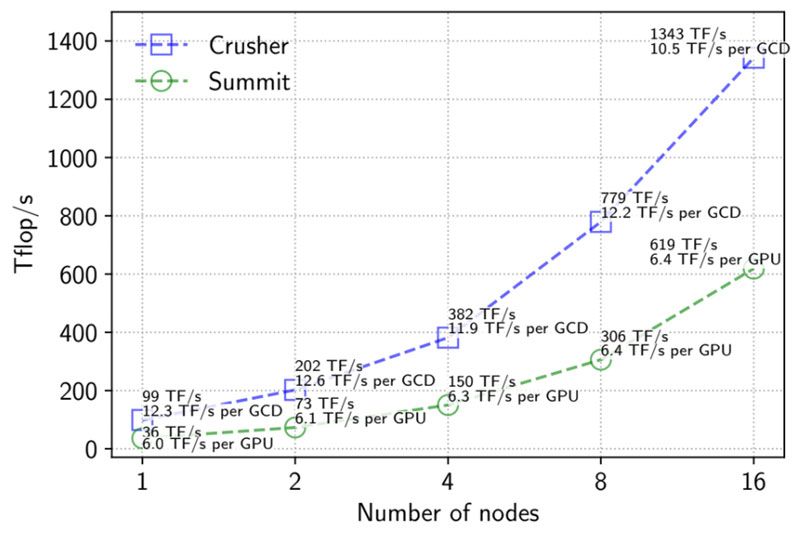
Figure 6. Weak-scaling performance of SLATE’s double-precision gemm operation on Summit and Crusher.

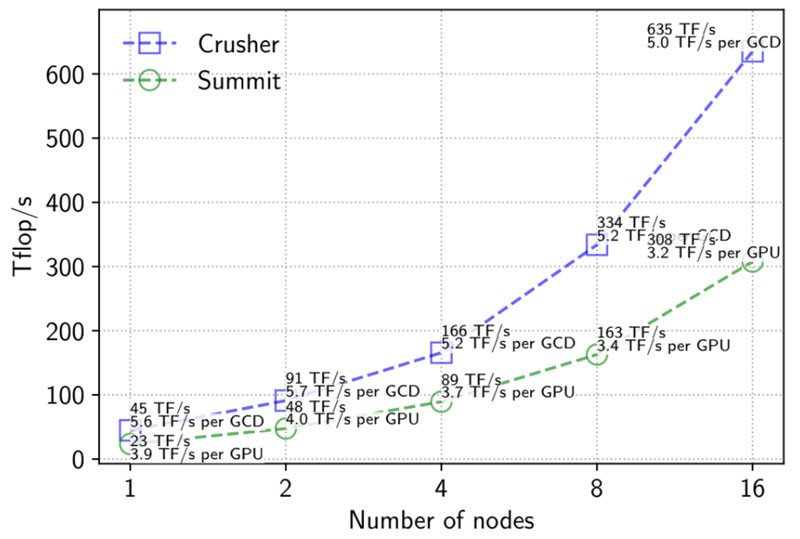
Figure 7. Weak-scaling performance of SLATE’s double-precision potrf operation on Summit and Crusher.

Other Minor Porting Discrepancies

The team noted that only minor differences between NVIDIA’s CUDA and AMD’s HIP (Heterogeneous Interface for Portability) arose when porting to AMD GPUs. For example, the AMD implementation of the complex abs() function is not numerically robust for numbers with intermediate overflow.[10] Consequently, the SLATE team substituted an implementation based on LAPACK. Similarly, however, a multiply in-place operation (x *= y) generated a compiler error for complex numbers. To fix this problem, the team simply changed the expression to x = x *y.

For Intel GPUs, the queuing mechanism used by SYCL is set by default to out-of-order execution. This default setting can cause issues in enforcing the data dependencies in the DAG, so the team easily corrected this issue by using the in_order property to initialize the SYCL queues.

Ginkgo

Ginkgo is a novel sparse numerical linear algebra framework written in C++ that began as part of the ECP CLOVER project. Use of the C++ programming language gave the team tremendous freedom in creating a state-of-the-art numerical library. In the team’s paper, “Ginkgo—A Math Library Designed for Platform Portability,” they acknowledged this flexibility: “We have the burden and privilege to start from scratch and to apply the lessons learned in other software projects.”[11] Anzt noted that the Ginkgo framework incorporates lessons learned about software interoperability from two other ECP projects, namely E4S and the xSDK library, both of which have been available for many years. To help guide the projects, the team designed the framework according to the SOLID software design principles:

Single responsibility,
Open/closed,
Liskov substitution,
Interface segregation, and
Dependency inversion.

Ginkgo is an open-source community effort that operates under the modified BSD (Berkeley Software Distribution) license. Part of the novelty of the Ginkgo design is that everything is expressed as a linear algebra operator.[12] This approach naturally fits with how mathematicians and computer scientists think about their problems and, as a result, enhances user-friendliness and reduces coding effort.

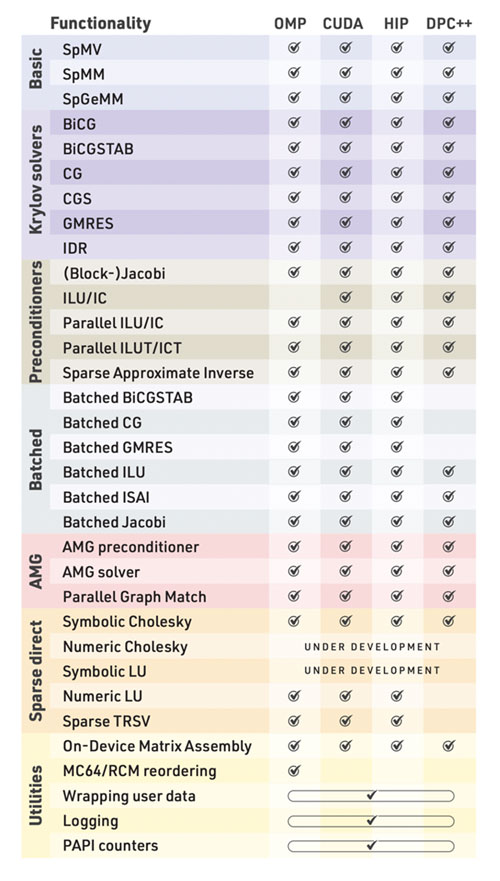
Ginkgo also provides numerous building blocks (e.g., sparse matrix-vector product) for a variety of matrix formats, iterative solvers, and preconditioners (Figure 8).

Figure 8. Functionality implemented by Ginkgo.

Specifying the matrix format is particularly important because the choice of sparse matrix format can have drastic performance implications. The selection process also dovetails nicely with C++ to call optimized back-end implementations for CPUs and GPUs and to enable writing new back ends for yet-to-be-designed HPC devices. Essentially, C++ polymorphism (i.e., the ability to call variants of the same method or C++ object depending on the type[s] of variables passed to the method) provides Ginkgo developers with a natural, programmer-friendly way to organize their code and support different back ends to call vendor-optimized libraries.

“The design choice to use a back-end model,” Anzt explained, “was motivated by a desire for the framework to achieve near-peak performance without sacrificing portability.” Kokkos inspired the design because it delivers both portability and performance. Unlike Kokkos, the Ginkgo framework focuses exclusively on sparse linear algebra. The SLATE framework uses a back-end model because it enables the software to call vendor- and hardware-specific libraries. Along with the targeted performance benefits, this design decision means that Ginkgo’s many users do not need to wait for Kokkos to add new features. Ginkgo currently supports back ends for AMD GPUs, Intel CPUs and GPUs, NVIDIA GPUs, and other OpenMP-supported architectures (Figure 9).

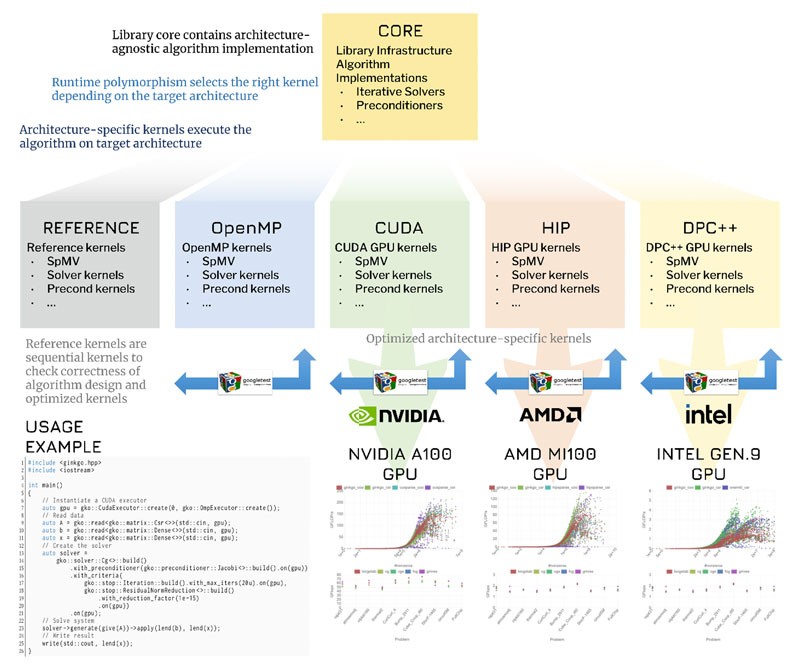
Figure 9. Ginkgo is based on a universal linear operator abstraction. It uses C++ polymorphism to target a variety of CPU and GPU back ends and is extensible for future architectures.

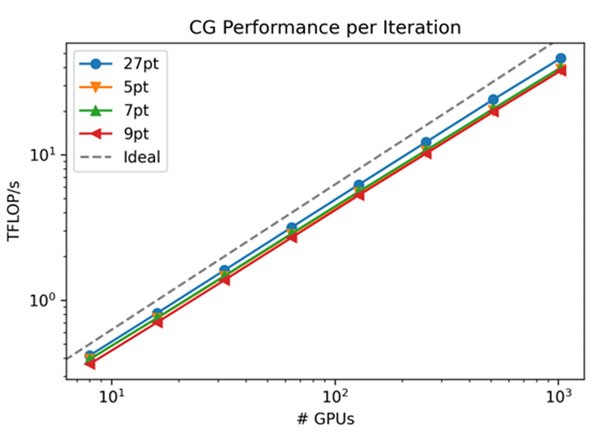
The benchmark results in Figures 10 and 11 demonstrate Ginkgo’s achievement of near-peak performance without sacrificing portability. These results, obtained on the Crusher test bed, indicate the performance that the full Frontier exascale supercomputer might achieve. Note the closeness of the observed performance relative to the ideal performance and scaling behavior shown by the black-dashed line (Figure 10).

Figure 10. Ginkgo performance on each iteration of a conjugate-gradient (CG) benchmark.

The team reported excellent cross-platform performance and noted, “On all hardware, Ginkgo’s SPMV [sparse matrix-vector multiplication] kernels are competitive with the vendor libraries, indicating the validity of the library design and demonstrating good performance portability.”[13]

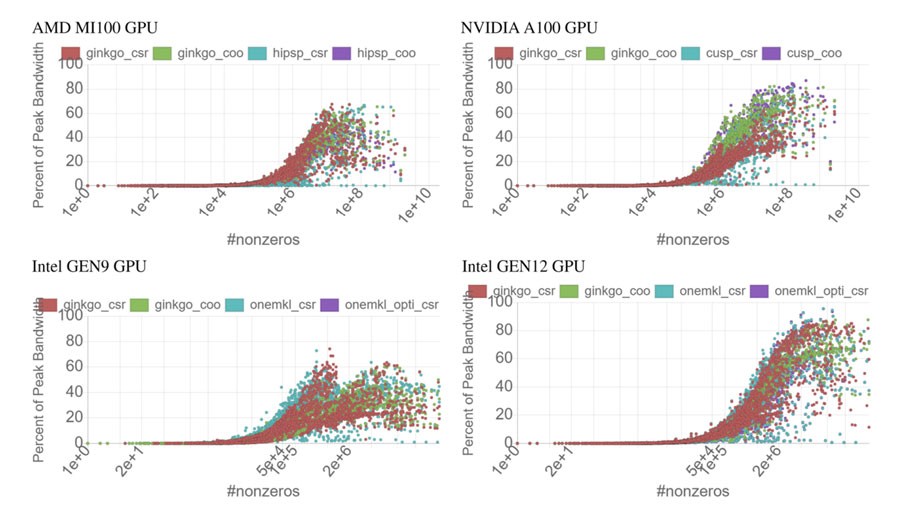
Figure 11. Cross-platform performance results as of 2022. (Source)

A key advance in Ginkgo, according to Anzt, is the decoupling of memory precision from arithmetic precision. The recent inclusion of hardware support for reduced-precision arithmetic in CPUs and GPUs to speed up machine-learning applications also makes this capability available for numerical libraries. Mixed-precision arithmetic with hardware support is now available on both GPUs and CPUs because of the massive adoption of machine learning by commercial and scientific communities. This general availability enables the global HPC community to leverage the performance and power savings of mixed-precision arithmetic.

Anzt has been advocating the benefits of mixed-precision arithmetic for many years. For example, in 2020, he wrote the article, “Towards Use of Mixed Precision in ECP Math Libraries.” Other HPC libraries, such as the Hierarchical Computations on Manycore Architectures (HiCMA) library developed by the HiCMA research group at King Abdullah University of Science and Technology, also exploit the capabilities of mixed-precision arithmetic operations.[14] The recent Gordon Bell Prize finalist paper, “Reshaping Geostatistical Modeling and Prediction for Extreme-Scale Environmental Applications,” utilized HiCMA and mixed-precision arithmetic to reach impressive performance while preserving the accuracy of ExaGeoStat, a high-performance computational software for geostatistical and environmental applications.[15]

Anzt noted that many algorithms are overprovisioned for flop/s (floating-point operations per second). Instead, he advocates using double precision for math and lower precision when accessing memory. The Ginkgo linear operators are flexible and allow for reduced precision and even compressed-storage formats. “With the bandwidth savings, especially for sparse matrix operations,” Anzt said, “you win in the end.”

With the bandwidth savings, especially for sparse matrix operations, you win in the end. — Hartwig Anzt

Reduced-precision arithmetic has proven effective—as has Anzt’s coordination of the effort. In 2019, on an episode of the Let’s Talk Exascale podcast, “The Ginkgo Library Project Is Developing a Vision for Multiprecision Algorithms,” ECP Communications Specialist Scott Gibson explained, “Several math library projects recently began looking into abandoning the strict IEEE double-precision paradigm and investigating the potential of mixing different precision formats to benefit from faster computation and communication in a lower-precision format. Instead of having different projects independently researching on multiprecision algorithms, ECP decided to synchronize these efforts and channel the activities [. . .] with Anzt as the coordinator.”

For more information about Ginkgo, see the following:

heFFTe: FFTs with Performance

The heFFTe library provides good (i.e., linear) scalability for FFT operations on computational clusters with large node counts, is available as open-source software, and contains C++ and CUDA kernels with a CUDA-aware MPI and OpenMP interface for communication.

Development of heFFTe was motivated by the heFFTe team’s observation that “the current state-of-the-art FFT libraries are not scalable on large heterogenous machines with many nodes or even on one node with multiple high-performance GPUs (e.g., several NVIDIA V100 GPUs). Furthermore, these libraries require large FFTs to deliver acceptable performance on one GPU. Efforts to simply enhance classical and existing FFT packages with optimization tools and techniques—such as autotuning and code generation—have so far not been able to provide an efficient, high-performance FFT library capable of harnessing the power of supercomputers with heterogenous GPU-accelerated nodes. In particular, ECP applications that require FFT-based solvers might suffer from the lack of fast and scalable 3D FFT routines for distributed heterogenous parallel systems, which is the very type of system that will be used in upcoming exascale machines.”[16]

The current state-of-the-art FFT libraries are not scalable on large heterogenous machines with many nodes or even on one node with multiple high-performance GPUs (e.g., several NVIDIA V100 GPUs). Furthermore, these libraries require large FFTs to deliver acceptable performance on one GPU. Efforts to simply enhance classical and existing FFT packages with optimization tools and techniques—such as autotuning and code generation—have so far not been able to provide an efficient, high-performance FFT library capable of harnessing the power of supercomputers with heterogenous GPU-accelerated nodes. In particular, ECP applications that require FFT-based solvers might suffer from the lack of fast and scalable 3D FFT routines for distributed heterogenous parallel systems, which is the very type of system that will be used in upcoming exascale machines. — https://icl.utk.edu/fft/

Jack Dongarra—2021 recipient of the ACM (Association for Computing Machinery) Turing Award and University Distinguished Professor of Computer Science in the EECS department at the University of Tennessee, Knoxville—said, “heFFTe reduces FFT to a communications problem.”

heFFTe reduces FFT to a communications problem. — Jack Dongarra

Thus, MPI scaling performance tends to dictate the performance and scaling behavior of heFFTe. Significant work has been devoted to making MPI run as fast as possible on supercomputers, and this work bodes well for applications that use heFFTe on US exascale supercomputers. Figure 12 shows the FFT internode communication bandwidth achieved on Spock, which is a test bed system for the Frontier exascale supercomputer.

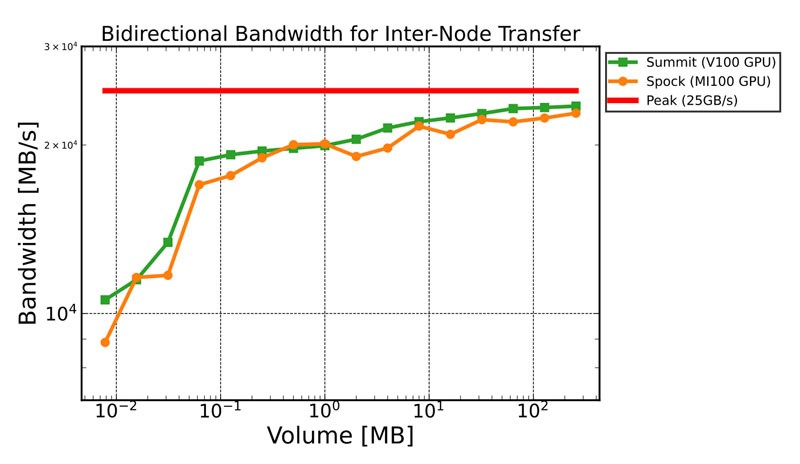
Figure 12. FFT internode communication bandwidth achieved on Summit with NVIDIA V100 GPUs vs. Spock with AMD MI100 GPUs.

The use cases for heFFTe are many and include accelerated

simulations for molecular dynamics,
applications for many-body dynamics,
partial differential equation (PDE) solvers, and
applications for PDE image and signal processing.

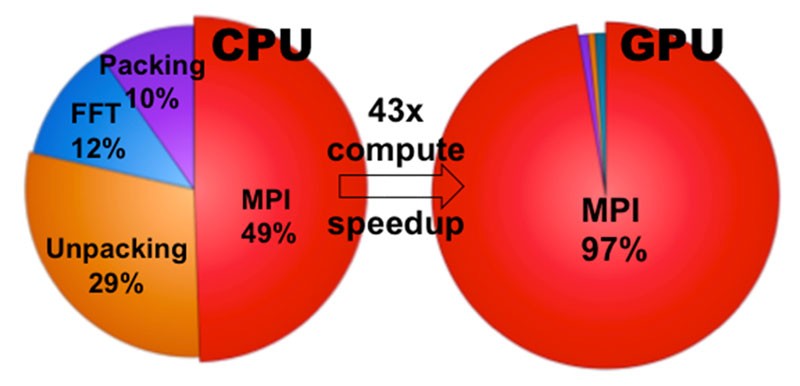
The performance results are significant (Figure 13) and demonstrate that local 3D FFT computations are accelerated by over 40× when using GPUs compared with multicore CPUs. Furthermore, heFFTe supports various architectures (e.g., NVIDIA, AMD, and Intel GPUs) with different back ends. Along with Ginkgo, heFFTe demonstrates the success of using a back-end model for targeted HPC applications and libraries.

Figure 13. A comparison that shows that heFFTe can deliver a >40× speedup over a CPU.

According to Anzt, one motivation for using hardware-targeted back ends is that general parallel run times (e.g., OpenMP) use prefetching to speed up sequential memory accesses. FFTs exhibit irregular memory accesses, and the back end must account for this irregularity to make the best use of the device’s memory bandwidth. Like Ginkgo, heFFTe supports mixed-precision arithmetic and compression to further accelerate memory accesses and increase performance.

For more information about heFFTe, see the following:

Ayala, S. Tomov, A. Haidar, and J. Dongarra, “heFFTe: Highly Efficient FFT for Exascale,” In Computational Science – ICCS 2020 (June 2020): 262–75, https://doi.org/10.1007/978-3-030-50371-0_19.
Ayala, S. Tomov, M. Stoyanov, and J. Dongarra, “Scalability Issues in FFT Computation,” In Parallel Computing Technologies PaCT 2021 (September 2021): 279–87, https://doi.org/10.1007/978-3-030-86359-3_21.
Sharp, M. Stoyanov, S. Tomov, and J. Dongarra, “A More Portable HeFFTe: Implementing a Fallback Algorithm for Scalable Fourier Transforms,” 2021 IEEE High Performance Extreme Computing Conference (HPEC) (2021): 1–5, https://doi.org/10.1109/HPEC49654.2021.9622811.
Ayala, S. Tomov, P. Luszczek, S. Cayrols, G. Ragghianti, and J. Dongarra, “Analysis of the Communication and Computation Cost of FFT Libraries towards Exascale,” ICL Technical Report, ICL-UT-22-07, 2022,
https://icl.utk.edu/files/publications/2022/icl-utk-1558-2022.pdf.
Cayrols, J. Li, G. Bosilca, S. Tomov, A. Ayala, and J. Dongarra, “Mixed Precision and Approximate 3D FFTs: Speed for Accuracy Trade-Off with GPU-Aware MPI and Run-Time Data Compression,” ICL Technical Report, ICL-UT-22-04, May 2022,
https://icl.utk.edu/files/publications/2022/icl-utk-1555-2022.pdf.

Summary

The CLOVER project reflects many lessons learned in designing performance-portable numerical libraries. As Anzt observed, “community efforts and good software design are essential to software sustainability, and they pay off in the long run. The decision to spend half the ECP funding on software was worth the investment.”

This research was supported by the Exascale Computing Project (17-SC-20-SC), a joint project of the U.S. Department of Energy’s Office of Science and National Nuclear Security Administration, responsible for delivering a capable exascale ecosystem, including software, applications, and hardware technology, to support the nation’s exascale computing imperative.

Rob Farber is a global technology consultant and author with an extensive background in HPC and machine learning technology.

[1] https://libensemble.readthedocs.io/en/develop/platforms/spock_crusher.html

[2] https://docs.olcf.ornl.gov/systems/crusher_quick_start_guide.html

[3] https://ieeexplore.ieee.org/document/6156851

[4] https://en.wikipedia.org/wiki/Fast_Fourier_transform

[5] https://icl.utk.edu/fft/

[6] ibid

[7] https://icl.utk.edu/slate/

[8] https://icl.utk.edu/files/publications/2020/icl-utk-1390-2020.pdf

[9] https://netlib.org/utk/people/JackDongarra/PAPERS/icl-utk-1351-2019.pdf

[10] https://sc22.supercomputing.org/presentation/?id=ws_p3hpc116&sess=sess428

[11] https://arxiv.org/abs/2011.08879