A team of scientists working with the ExaGraph Co-Design Center provided a review of work done under the Exascale Computing Project (ECP) to optimize combinatorial and graph algorithms and related software development for scaling to exascale applications. The summary focuses on their recent efforts in porting the algorithms to GPU architectures and covers combinatorial and algebraic methods. The scientists’ work was published as a Special Issue article in the September 2021 issue of the SAGE International Journal of High Performance Computing Applications.
Graph algorithms are hard to scale due to their sparse and irregular memory access patterns, low computation-to-communication ratios, and inherently serial algorithms, and exascale computing systems with billions of CPU and GPU hardware threads pose extreme challenges in scaling graph algorithms. ExaGraph uses combinatorial and algebraic approaches to develop state-of-the-art algorithms, software implementations, and application integration for several graph algorithms. Efforts have resulted in several novel approximation algorithms and integration of graph algorithms in codes for applications such as bioinformatics, wind energy, and computational chemistry. For several graph problems (e.g., influence maximization, b-matching, graph partitioning, graph clustering), the parallel algorithms and scalable implementations developed by the ExaGraph team are the current-best or only tools available. Integration of the new capabilities into application codes has resulted in significant speedups and scaling on preexascale and forthcoming exascale systems.
These advancements facilitate new capabilities such as use within ECP-developed NWChemEx chemistry code of a parallel 1/3-approximation algorithm for submodular b-matching to perform load-balanced block assignment in the Fock matrix build. The algorithm provides superior performance and enables scaling of NWChemEx to a larger number of processors. Since publication, the team has produced additional algorithmic results, software optimizations, and applications. For example, a multiobjective graph-matching algorithm developed for the aggregation-based Algebraic MultiGrid (AMG) solver computes effective preconditioners in the presence of anisotropy, reducing solve and setup times, number of iterations, and operator complexity for several inputs.
S. Acer, A. Azad, E.G. Boman, A. Buluç, K.D. Devine, S.M. Ferdous, N. Gawande, S. Ghosh, M. Halappanavar, A. Kalyanaraman, A. Khan, M. Minutoli, A. Pothen, S. Rajamanickam, O. Selvitopi, N.R. Tallent, and A. Tumeo. “EXAGRAPH: Graph and Combinatorial Methods for Enabling Exascale Applications.” 2021. International Journal of High Performance Computing Applications (September).
https://doi.org/10.1177/10943420211029299
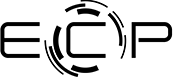
Scaling results for CuRipples. A speedup of up to 790× was achieved over a state-of-the-art serial implementation (leftmost bar), with significant improvements to the approximation factor (to ε = 0.13) and doubling of the number of seeds (right). The input network was com-Orkut. Details are available in Minutoli et al. (2020a).