Project Details
Efficient exploitation of exascale architectures requires rethinking of the numerical algorithms for solving partial differential equations (PDEs) on general unstructured grids. New architectures, such as general-purpose graphics processing units (GPUs) favor algorithms that expose ultra fine-grain parallelism and maximize the ratio of floating point operations to energy intensive data movement.

FIGURE 1: Examples of compressible (left) and incompressible (right) flow simulations with high-order finite elements.
Many large-scale PDE-based applications employ unstructured finite element discretization methods, where practical efficiency is measured by the accuracy achieved per unit computational time. One of the few viable approaches to achieve high performance in this case is to use matrix-free high-order finite element methods, since these methods can both increase the accuracy and/or lower the computational time due to reduced data motion. To achieve this efficiency, high-order methods use mesh elements that are mapped from canonical reference elements (hexahedra, wedges, pyramids, tetrahedra) and exploit, where possible, the tensor-product structure of the canonical mesh elements and finite element spaces. Through matrix-free partial assembly, the use of canonical reference elements enables substantial cache efficiency and minimizes extraneous data movement in comparison to traditional low-order approaches.
The Center for Efficient Exascale Discretizations (CEED) is a focused team effort within the U.S. Department of Energy (DOE) Exascale Computing Project (ECP) that aims to develop the next-generation discretization software and algorithms to enable a wide range of finite element applications to run efficiently on future hardware. CEED is a research partnership involving more than 30 computational scientists from two DOE labs and five universities, including members of the MFEM, Nek5000, MAGMA and PETSc projects.
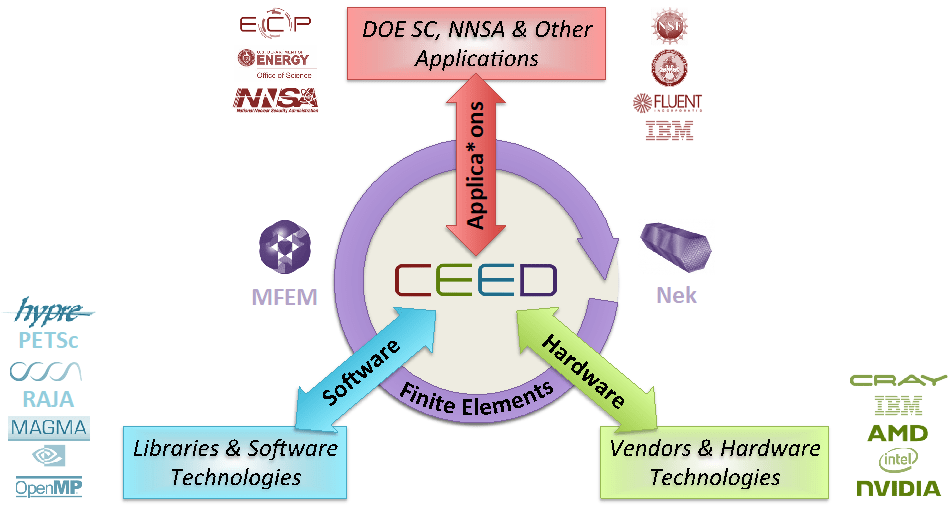
FIGURE 2: The CEED co-design center interacts with applications, software technologies projects and ECP vendors.
Following the ECP co-design philosophy, CEED is positioned as a computational motif hub between applications, hardware vendors and software technologies projects. As such, the main objectives of the project are to:
1. Help applications leverage future architectures by providing them with state-of-the-art discretization algorithms that better exploit the hardware and deliver a significant performance gain over conventional low-order methods.
2. Collaborate with hardware vendors and software technologies projects to utilize and impact the upcoming exascale hardware and its software stack through CEED-developed proxies and miniapps.
3. Provide an efficient and user-friendly unstructured PDE discretization component for the upcoming exascale software ecosystem.
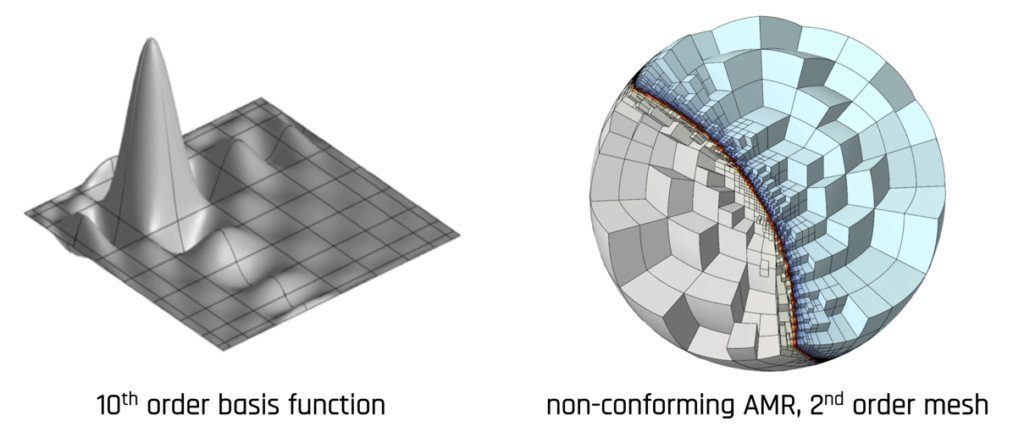
FIGURE 3: High-order finite element basis function (left) and a high-order mesh with local non-conforming adaptive meh refinement (right).
To address these objectives, the center’s co-design efforts are organized in 4 interconnected research and development thrusts, focused on the following computational motifs and their performance on exascale hardware:
PDE-based simulations on unstructured grids. CEED is producing a range of software products supporting general finite element algorithms on triangular, quadrilateral, tetrahedral and hexahedral meshes. A full range of topological spaces and discretizations are encompassed, including conforming and non-conforming unstructured adaptive mesh refinement (AMR).
High-order/spectral finite elements. CEED algorithms and software come with comprehensive high-order support, with efficient matrix-free operator evaluation for any order space on any order mesh, including high-order curved meshes and all geometries. The CEED software also includes optimized assembly support for low-order methods.
All CEED-developed software is open-source and is freely available on GitHub at https://github.com/ceed.
For more information, visit https://ceed.exascaleproject.org.

