By Rob Farber, contributing writer
Structured Matrix Package (STRUMPACK) is a portable software library that provides linear algebra routines and linear system solvers for sparse and dense rank-structured linear systems that runs well on many-core processors and GPUs. In short, STRUMPACK focuses on efficiently performing dense linear algebra on relatively small submatrices in the global matrix. Portable programming paradigms that can run well on both CPUs and GPUs are crucial to the efficient use of modern large-scale compute platforms. According to Dr. Xiaoye S. “Sherry” Li, a senior scientist and group lead at Lawrence Berkeley National Laboratory, “The internal representation explains why STRUMPACK can deliver higher performance and lower memory consumption. The lower memory consumption is a big deal, especially for GPUs.”
“The internal representation explains why STRUMPACK can deliver higher performance and lower memory consumption. The lower memory consumption is a big deal, especially for GPUs.” — Dr. Sherry Li
NVIDIA GPUs and many CPU types are currently supported. Dr. Li said that the team also recently started working with AMD GPUs.
The STRUMPACK library is closely related to the SuperLU library, both of which provide direct solvers for sparse linear systems. The former targets symmetric-patterned sparse linear systems, whereas the latter targets nonsymmetric linear systems.
Benefits of the STRUMPACK Algorithm and Internal Representation
One of STRUMPACK’s goals is to deliver direct solvers and preconditioners based on a multifrontal variant of sparse Gaussian elimination. Partial pivoting for numerical stability is widely used in dense systems, swapping rows at each elimination step to place large elements on the diagonal. In the sparse case, this incurs a relatively larger amount of data movement and requires the dynamic management of data structures, severely hampering parallel scalability. Instead, STRUMPACK and the related SuperLU library use a static pivoting strategy in which the matrix is permuted beforehand so that the largest elements of the input matrix are placed on the diagonal instead of swapping at runtime.[1]
Using multifrontal sparse elimination, STRUMPACK’s internal operations are mostly based on dense matrix kernels, resulting in high performance on both CPUs and GPUs.
Compression Provides Drastic Memory Savings
Additional and drastic memory savings, even for numerically challenging problems, are achieved through compression by using the zfp library. Compression enables the solution of larger problems with manageable errors while incurring a small overhead during factorization. Compression and decompression can both be offloaded to the GPU.[2] Figure 1 provides an example of the dramatic memory savings that can be achieved by using compression on a 3D 603 complex Helmholtz problem.
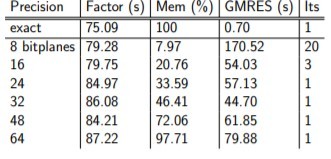
Figure 1: Example of the dramatic memory savings that can be achieved using compression on a 3D 603 complex Helmholtz problem. (Source: https://ecpannualmeeting.com/assets/overview/posters/ECP2020_STRUMPACK_ButterflyPACK.pdf.)
zfp is a compressed representation of multidimensional floating-point arrays that are ubiquitous in high-performance computing (HPC). “It was designed to reduce the memory footprint and offline storage of large arrays, as well as to reduce data movement by effectively using fewer bits to represent numerical values,” said Peter Lindstrom of Lawrence Livermore National Laboratory, who manages all activities related to the zfp project. “zfp can sometimes provide six to seven orders of magnitude higher accuracy than conventional floating-point representations for the same, or even less, amount of storage.”[3]
Added Functionality Including Preconditioners and Direct Solvers
Along with portability, STRUMPACK leverages its internal hierarchical matrix algebra to add features such as scalable preconditioners in addition to the ability to act as an exact direct solver.
“Preconditioners are an important addition to STRUMPACK because direct solvers use a lot of memory and consume many flops,” Li said. “The STRUMPACK preconditioner uses less memory and burns fewer flops. It’s a bridge or an ‘approximate direct solver.’” The STRUMPACK documentation provides more information on the compression strategies and tuning to obtain a good preconditioner for a specific problem.[4]
“Preconditioners are an important addition to STRUMPACK because direct solvers use a lot of memory and consume many flops. The STRUMPACK preconditioner uses less memory and burns fewer flops.” — Dr. Sherry Li
When desired, as noted in the github page notes, “the sparse solver in STRUMPACK can also be used as an exact direct solver, in which case it functions similarly as, for instance, SuperLU_DIST. The STRUMPACK sparse direct solver delivers good performance and distributed memory scalability and provides excellent CUDA support, ” Li said.
From a technical point of view, the sparse linear solve algorithms in STRUMPACK exploit different dense rank-structured matrix formats[5] to perform a type of compression (e.g., compress the fill-in). This leads to purely algebraic, fast, and scalable—both with problem size and compute cores—approximate direct solvers or preconditioners. These preconditioners are mostly aimed at large sparse linear systems that result from the discretization of a partial differential equation but are not limited to any particular type of problem. STRUMPACK also provides preconditioned generalized minimal residual method and biconjugate gradient stabilized method iterative solvers.
The ability to work with dense rank-structured matrices supports Toeplitz, Cauchy, boundary element method, QuantumChem, machine learning, covariance, and numerous other applications.
STRUMPACK as a Multifrontal Rank-Structured Preconditioner
As a multifrontal rank-structured preconditioner, STRUMPACK allows for the approximation of the largest fronts. Partitioning uses the recursive bisection of the separator by using a Metis partitioner, which can reduce computation on off-diagonal low-rank blocks. Tuning is achieved by using an ε compression tolerance plus the definition of the minimum front size for compression. Figure 2 shows examples of wavefronts.
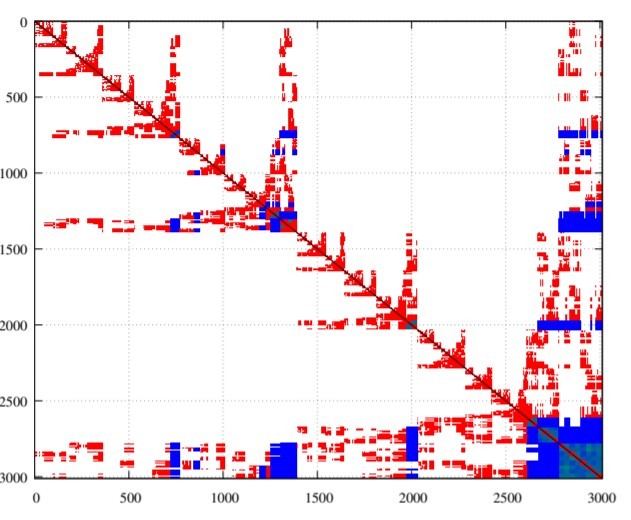
Figure 2: Example showing wavefronts. (Source: https://ecpannualmeeting.com/assets/overview/posters/ECP2020_STRUMPACK_ButterflyPACK.pdf.)
STRUMPACK includes C++ interfaces to the ButterflyPACK Fortran library to provide Hierarchically Off-Diagonal Butterfly formats. GPU acceleration leverages the capabilities of the cuBLAS, cuSOLVER, Software for Linear Algebra Targeting Exascale (SLATE), and Matrix Algebra on GPU and Multicore Architectures (MAGMA) libraries.
Summary
STRUMPACK is an Extreme-Scale Scientific Software Stack (E4S) project that provides robust and scalable factorization-based methods for the ill-conditioned and indefinite systems of equations that arise in high-fidelity, large-scale multiphysics and multiscale models. It also provides fast and scalable matrix operations for emerging artificial intelligence and machine learning applications.
E4S.io provides more information on using the tested and verified versions of STRUMPACK via the E4S containers or turnkey E4S build cache. A variety of processors, GPUs, and Linux operating system versions are supported. Users can also build the library via the E4S build from-source or directly from github.
Progress to Date
The STRUMPACK team’s publications provide information on the latest runtime and memory savings.
As of January 2021, the team has released STRUMPACK version 5.0.0 with improvements in the scalability of the hierarchical matrix algorithms—the dense hierarchical matrix compression is up to 4.7× faster on eight nodes of Cori-Haswell and 2.4× faster on Cori Knight’s Landing (KNL) nodes, whereas the hierarchical sparse factorization is up to 2.2× faster on eight Cori KNL nodes—and improvements in the hierarchical solve to reduce communication and more OpenMP support, leading to a 7× faster matrix redistribution and 1.4× faster solve.
STRUMPACK version 5.0.0 also includes GPU support using CUDA and SLATE, leading to over a 10× performance improvement compared with CPU-only code running on four Summit nodes. This latest version also introduces support for the block low-rank structured matrix format and a preconditioner based on the approximate multifrontal factorization by using this block low-rank compression. The new preconditioner is highly robust, even for numerically very challenging problems, such as those arising from high-frequency wave equations.
Rob Farber is a global technology consultant and author with an extensive background in HPC and machine learning technology development that he applies at national labs and commercial organizations. Rob can be reached at [email protected].
[1] ECP, “Exagraph Collaboration with STRUMPACK/SUPERLU: Factorization-Based Sparse Solvers and Preconditioners for Exascale,” August 2018, https://www.exascaleproject.org/exagraph-with-strumpack-superlu/.
[2] P. Ghysels, Y. Liu, and X. S. Liu, “STRUMPACK & Butterfly PACK,” https://ecpannualmeeting.com/assets/overview/posters/ECP2020_STRUMPACK_ButterflyPACK.pdf.
[3] “Reducing the Memory Footprint and Data Movement on Exascale Systems,” April 2020, https://www.exascaleproject.org/reducing-the-memory-footprint-and-data-movement-on-exascale-systems/.
[4] “STRUMPACK STRUctured Matrix PACKage, https://portal.nersc.gov/project/sparse/strumpack/v5.0.0/algorithm.html.
[5] STRUMPACK currently has support for the Hierarchically Semi-Separable, Block Low Rank, Hierarchically Off-Diagonal Low Rank, Butterfly, and Hierarchically Off-Diagonal Butterfly rank-structured matrix formats (source sy).